Teresa Carrillo Ramírez
División de Matemáticas e Ingeniería, Facultad de Estudios Superiores Acatlán UNAM.
Antecedentes
En marzo de 2020, tras la declaración de la pandemia de COVID que llevo a las escuelas a cambiar de modalidad presencial a clases virtuales; los docentes y los estudiantes nos enfrentamos tanto a un proceso de adaptación, como a un cambio de paradigmas en los procesos de enseñanza aprendizaje.
La asignatura de Métodos Numéricos en la Licenciatura de Matemáticas Aplicadas y Computación requiere que el alumno sustente matemáticamente los métodos, identifique sus aplicaciones y los implemente en programas de computadora, para resolver problemas prácticos. Lo anterior requiere que el docente defina estrategias de enseñanza que, además de trasmitir conocimientos, desarrollen en el estudiante actitudes y habilidades para lograr un aprendizaje autónomo y significativo.
Lo anterior implica mejorar la relación docente-estudiante-aprendizaje, ya que “el reto del docente es enseñar matemáticas de una forma diferente, interactiva, dinámica y contextualizada, en donde la tecnología se convierte en una herramienta fundamental” (Muñoz Suárez, Porras Fernández, & Maylya, 2017).
En este trabajo se presentan los resultados de la incorporación del uso de Geogebra en las estrategias de enseñanza-aprendizaje del curso de Métodos Numéricos I, mismo que se impartió de forma virtual con apoyo de Moodle y Zoom. El objetivo es promover el aprendizaje autónomo, mantener el interés y la motivación en las clases virtuales, al mismo tiempo de mejorar el aprovechamiento reflejado en las calificaciones finales. Ya que, cómo los menciona Estéfano (2013, pp 21-38), lo importante es enseñar a los estudiantes a ser aprendices estratégicos, lo que requiere un docente estratégico.
La metodología empleada involucra factores cuantitativos (percepción de los estudiantes) y cualitativos (análisis de las evaluaciones y calificaciones finales). Al trabajar en grupos de alumnos inscritos en los grupos de estudio, se trata de un diseño no experimental.
Uso de Geogebra para la enseñanza de métodos numéricos
Dado que “el docente es el responsable de seleccionar estrategias adecuadas para contribuir con el alumno en el desarrollo de competencias que le permitan lograr el perfil esperado” (Montero, Pedroza, Astiz, & Vilanova, 2015), se desarrollaron estrategias de enseñanza aprendizaje para el ciclo 2021-1 dentro de las que se incorporaron las direcciones que indica Cabrera Ruíz (2009) para el desarrollo de la autonomía en el aprendizaje con el apoyo de Geogebra.
Geogebra es un software matemático gratuito con fines educativos que se puede ejecutar en línea o instalarse en los dispositivos, por lo que es de fácil acceso. Además, es sencillo de utilizar, lo que lo hace ideal para su uso en las clases virtuales.
Enseñar a distancia, según Barberá, Badia y Mominó (2001) implica no solo promover la construcción del conocimiento en la memoria del estudiante, sino impulsar el desarrollo de habilidades y procesos cognitivos mediante los cuales se produce la construcción de ese conocimiento, a partir de lo anterior, para cada método se llevó la siguiente secuencia
- Presentación de la clase
- Exposición del método
- Aplicación del método con Geogebra
- Prueba del material con distintas condiciones
- Actividad de evaluación formativa con el uso de Geogebra.
Estrategias de enseñanza virtual en alumnos de licenciatura
En los cursos de métodos numéricos presenciales, que se imparte en el tercer semestre de la carrera, la exposición de los temas se hace con presentaciones y el apoyo del pizarrón para explicar sustento matemático, al mismo tiempo que se atienden las inquietudes de los alumnos. En la modalidad virtual, está dinámica se complica por la ausencia del lenguaje corporal, por lo que se recurrió a Geogebra para proporcionar al estudiante un objeto de aprendizaje que pueda manipular para probar diferentes condiciones y diferentes problemas, algunos ejemplos de las actividades elaboradas se muestran en la Figura 1.
Como se mencionó antes, el uso de Geogebra se integró en dos etapas: la exposición del tema y la evaluación formativa (ejercicios de práctica y reforzamiento). Al final del curso, se aplicó una encuesta de percepción sobre las estrategias de enseñanza y finalmente se realizaron comparativos de las calificaciones finales con los dos periodos anteriores, el 2019-1 (presencial) y el 2020-1 (de transición por el inicio de la pandemia).
Figura 1. Ejemplos de actividades en Geogebra
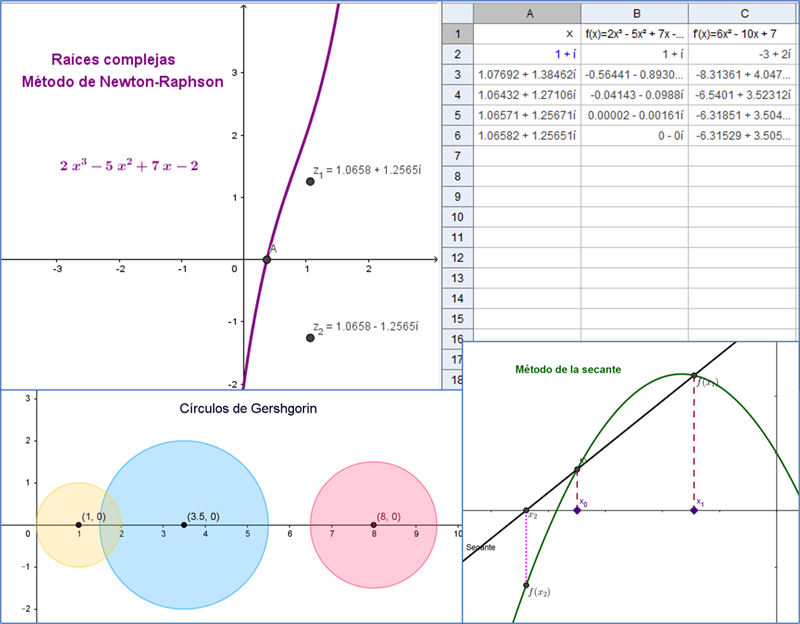
Resultados
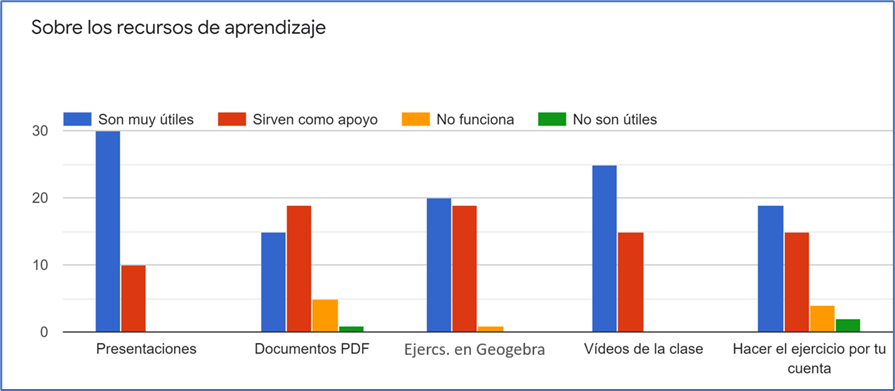
Como parte de los resultados de la encuesta de percepción, aplicada al final del curso, la Figura 2 muestra que los estudiantes consideran útiles todos los elementos empleados para la enseñanza, sin embargo, destacan las Presentaciones y los Vídeos de la clase (exposición del tema), seguidos de los Ejercicios en Geogebra.
Figura 2. Opinión sobre los recursos de enseñanza
Vale la pena destacar que los alumnos siempre mostraron interés durante las actividades con Geogebra, lo que sin duda es una motivación para el docente.
En lo que se refiere a los resultados en las calificaciones finales, la Figura 3 muestra las calificaciones de los tres últimos periodos en los que se impartió la asignatura. Puede observarse, que en el período en el que implementó el uso de Geogebra (2021-1), aumento el porcentaje de acreditados (A) con respecto a los dos periodos anteriores.
Figura 3. Calificaciones finales por semestre
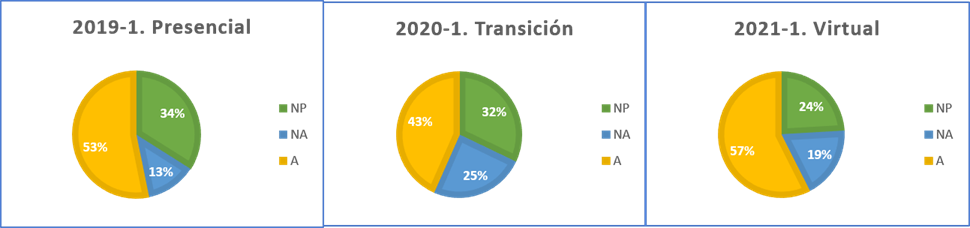
Es importante resaltar que disminuyó el porcentaje de alumnos que abandonan el curso (NP), con respecto a los dos cursos anteriores.
Conclusiones
El presente reporte permitió confirmar que un buen diseño de estrategias de enseñanza-aprendizaje que incorpore el uso de Geogebra para promover el aprendizaje autónomo y la motivación en estudiantes de Métodos Numéricos de la Licenciatura en Matemáticas Aplicadas y Computación, redundan en:
- Motivación e interés durante la clase, lo que redunda en la permanencia en el curso.
- Aprendizaje significativo
- Desarrollo de habilidades de aprendizaje autónomo
- Mejora en el desempeño (calificación final).
Siempre podrán mejorarse los recursos empleados y desarrollar nuevos a partir de la experiencia y las observaciones hechas por los estudiantes. Sin embargo, para tratarse de un primer acercamiento los resultados fueron bastante satisfactorios.
REFERENCIAS
La incógnita en la educación a distancia. Revista de Docencia Universitaria, 1(3). https://revistas.um.es/redu/article/view/11511
Autonomía en el aprendizaje: direcciones para el desarrollo en la formación profesional. Actualidades Investigativas en Educación, 9(2), 1-22. https://www.redalyc.org/pdf/447/44713058006.pdf
Entrenamiento de alumnos de educación superior en estrategias de aprendizaje en matemáticas. Psicothema, 18(3), 348-352. https://reunido.uniovi.es/index.php/PST/article/view/8440
Conocimiento y aplicación de estrategias de aprendizaje por profesores de educación superior a distancia. Zona próxima. Revista del Instituto de Estudios en Educación(19), 21-38. https://dialnet.unirioja.es/servlet/articulo?codigo=6416684
Caracterízación de las actitudes de estudiantes universitarios de Matemática hacia los métodos numéricos. Revista electrónica de investigación educativa, 17(1), 88-99. http://www.scielo.org.mx/scielo.php?pid=S1607-40412015000100006&script=sci_arttext
Aplicación de software matemático para el logro de aprendizajes el cálculo diferencial e integral, en estudiantes universitarios. Tercer Congreso Internacional de Ciencias Pedagógicas, (págs. 1295-1314). Guayaquil. https://dialnet.unirioja.es/servlet/articulo?codigo=7210620